
Introduction
All customer relationships eventually come to and end but if we can postpone the inevitable we can improve lifetime value along with our sales outlook.
A penney saved is a penny earned; customer acquisition costs are generally lower than retention costs. Knowing which customers are at risk of churning can aid in focusing marketing resources to retention which helps maximize the value of acquisition expenditures.
This article will explore using logistic regression to determine which customers are at risk of churning. We will use a simple dataset available on Kaggle. To avoid making this article into a short novel, information on the mechanics of logistic regression can be found in this article.
Loading the Dataset
First we will set some basic options and import the tidyverse package for data transformations. Then load the csv file with stringsAsFactors set to true to save a step later.
options(scipen = 999)
library(tidyverse)
ChurnData <- read.csv("Churn_Modelling.csv", stringsAsFactors = T)
summary(ChurnData)
ChurnData <- select(
ChurnData,
CustomerId,
CreditScore,
Geography,
Gender,
Age,
Tenure,
Balance,
NumOfProducts,
HasCrCard,
IsActiveMember,
EstimatedSalary,
Exited
)Since the customer’s sir name is unlikely to play a role in customer retention we will exclude that variable from consideration and select the remaining variables. There are no NA values so there is no need for imputation.
Class Balance
It is always good to check our class balances. That is the proportion of the class present in the dataset, in this case that means how many churned customers exist relative to customers who did not churn.
Where a class occurrence is very rare such as instances of credit card fraud relative to overall transactions it can be difficult to train a model because the easiest way to predict the class is simply to always guess that an instance is not the target class. It’s possible to achieve 98% accuracy given a class present in 2% of cases simply by always guessing non-class.
mean(ChurnData$Exited == 1)
> mean(ChurnData$Exited == 1)
[1] 0.203This dataset is composed of about 20% of the class. This is not ideal, but it could be worse so we will leave it as is for this example and see what kind of accuracy we get without providing weighting.
Model Selection
A good place to start for predicting customer churn, or any other two-class problem, is a logistic regression or binomial model. If we can get a respectable predictive accuracy with this simple model then it will have the benefit of interpretability.
This is particularly relevant for customer churn since it is often the case that a business will want to know what factors play a role in customers ending the relationship.
Feature Selection
Our next task is selecting appropriate features, the MASS package can be helpful in checking various configurations for the lowest AIC score.
First we will create a binomial glm (generalized linear model) with “Exited” as the response variable. This is a lightweight model so will use the stepAIC function to search in both directions with 10,000 steps or until it finishes.
library(MASS)
mod <- glm(
Exited ~ CreditScore + Geography + Gender + Age + Tenure + Balance +
NumOfProducts + HasCrCard + IsActiveMember + EstimatedSalary,
family = "binomial",
data = ChurnData
)
mod <- stepAIC(mod, direction = "both", steps = 10000)
summary(mod)Call:
glm(formula = Exited ~ CreditScore + Geography + Gender + Age +
Tenure + Balance + NumOfProducts + IsActiveMember, family = "binomial",
data = ChurnData)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.376667347 0.235940447 -14.312 < 0.0000000000000002 ***
CreditScore -0.000668170 0.000280314 -2.384 0.0171 *
GeographyGermany 0.774058893 0.067657508 11.441 < 0.0000000000000002 ***
GeographySpain 0.035864566 0.070625185 0.508 0.6116
GenderMale -0.529117847 0.054481703 -9.712 < 0.0000000000000002 ***
Age 0.072684500 0.002574758 28.230 < 0.0000000000000002 ***
Tenure -0.015954160 0.009349985 -1.706 0.0879 .
Balance 0.000002653 0.000000514 5.162 0.000000245 ***
NumOfProducts -0.100719348 0.047124456 -2.137 0.0326 *
IsActiveMember -1.075352000 0.057666510 -18.648 < 0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 10110 on 9999 degrees of freedom
Residual deviance: 8563 on 9990 degrees of freedom
AIC: 8583
Number of Fisher Scoring iterations: 5Based on AIC score the best model configuration includes all variables except EstimatedSalary and HasCrCard. Those are excluded from our model.
As a note of caution, relying on stepAIC to pick our variables is not a good practice for a real dataset but it does offer some guidance that can save us time. A better practice is to consider why each variable is being included or excluded, and to consider whether it is logically related to the outcome, and that the direction of the coefficient makes sense.
Tenure looks suspicious with its 0.1 significance level, but longevity is logically related customer churn. In this case the sign is negative suggesting that as tenure increases the odds of churn decrease. Since this is as expected we will leave it in for now. We can always test a model with it excluded later.
Variance Inflation Factor
The car package has a helpful function for looking at variance inflation, that is where multi collinearity is present in our selected variables. That is where two or more features are contributing to the some effect in the response variable.
library(car)
vif(mod) GVIF Df GVIF^(1/(2*Df))
CreditScore 1.001190 1 1.000595
Geography 1.216570 2 1.050230
Gender 1.003859 1 1.001928
Age 1.081447 1 1.039927
Tenure 1.001934 1 1.000967
Balance 1.291125 1 1.136277
NumOfProducts 1.078980 1 1.038740
IsActiveMember 1.077815 1 1.038179This is a well behaved dataset considering some of what is available on Kaggle. A score of 5 would be worrisome, 2 would be ok, and 10 would be a serious problem. Since we have no serious problems here we can move on.
Quantile Residuals
Since generalized linear models are linear models we need to check our assumption of normalcy. The easiest way to do this is to create a Q-Q Plot to check our quantile residuals.
qr.mod <- qresid(mod)
qqnorm(qr.mod, las=1)
qqline(qr.mod)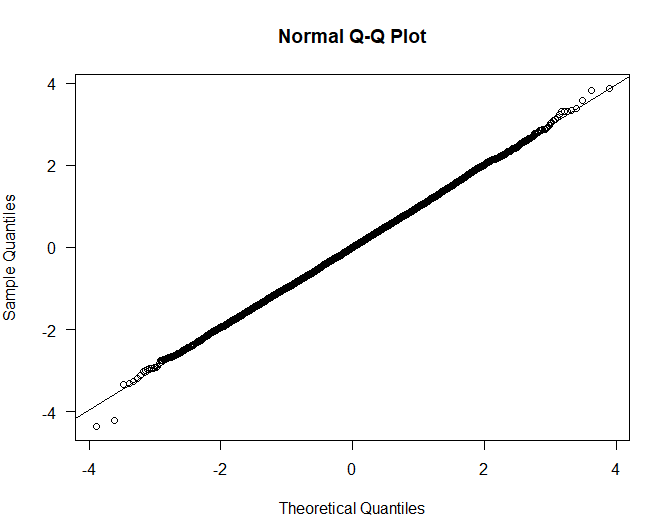
Everything is straight as an arrow across the diagonal, this looks like very normal data.
Residual Deviance
One quirk of logistic regression models that is not a concern in simple linear regression is overdispersion, that is where the assumption of constant variance is violated. One option to check this is to compare the residual deviance (or Pearson residuals) to the residual degrees of freedom to see if they are larger.
df.residual(mod) # Residual DF should be lower than
deviance(mod) # Residual Deviance
sum(resid(mod, type = "pearson")^2) # Pearson Residuals> df.residual(mod) # Residual DF should be lower than
[1] 9990
> deviance(mod) # Residual Deviance
[1] 8562.953
> sum(resid(mod, type = "pearson")^2) # Pearson Residuals
[1] 10090.08In this case our residual deviance is lower and our Pearson residuals are marginally higher, but it is not anywhere near a concerning difference.
Training Models
With the preliminary validation out of the way we can now get on to the fun of training our customer churn model.
We will use the caret package because it provides a much simpler interface than more modern packages such as mlr3 that use R6 classes. For splitting our data rsample from tidymodels provides a convenient function.
Since there are 10,000 observations we will stick with convention and use a 70/30 train and test split. The strata option ensures that the test split does not end up with all of the target class and botch our training.
#### Training and Test Split
library(caret)
library(rsample)
churn_split <- initial_split(ChurnData, prop=0.7, strata = "Exited")
train <- training(churn_split)
test <- testing(churn_split)Model Selection Revisited
This wouldn’t be data science if we weren’t testing a few models to see which performs best. We will test an ordinary binomial model and two penalized glmnet binomial models where one has the tenure variable and the other does not.
Ord.glm <- train(
factor(Exited) ~ CreditScore + Geography + Gender + Age + Tenure +
Balance + NumOfProducts + IsActiveMember,
data = train,
method = "glm",
family = "binomial",
preProc = c("zv", "center", "scale"),
trControl = trainControl(method = "cv", number = 10),
tuneLength = 20
)
Pen.glm.NoTenure <- train(
factor(Exited) ~ CreditScore + Geography + Gender + Age + Balance +
NumOfProducts + IsActiveMember,
data = train,
method = "glmnet",
family = "binomial",
preProc = c("zv", "center", "scale"),
trControl = trainControl(method = "cv", number = 10),
tuneLength = 20
)
Pen.glm <- train(
factor(Exited) ~ CreditScore + Geography + Gender + Age + Tenure + Balance +
NumOfProducts + IsActiveMember,
data = train,
method = "glmnet",
family = "binomial",
preProc = c("zv", "center", "scale"),
trControl = trainControl(method = "cv", number = 10),
tuneLength = 20
)
Pen.glm$bestTune
summary(resamples(list(
Pen.glm = Pen.glm, Pen.glm.NoTenure, Ord.glm = Ord.glm
)))$statistics$Accuracy Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
Pen.glm 0.8017118 0.8061516 0.8178571 0.8141135 0.8210714 0.8228571 0
Model2 0.8057143 0.8091334 0.8120100 0.8138315 0.8177912 0.8242857 0
Ord.glm 0.8014286 0.8085714 0.8100017 0.8126891 0.8198084 0.8228571 0Tuning shows consistent results and the penalized binomial model that includes Tenure indeed does have the best accuracy which was suggested by the lower AIC score for that configuration.
Receiver Operating Curve
The output for a two class problem is a probability between 0 and 1 which gives rise to the question of where the cutoff should be. A common approach to setting the cutoff is to use a Receiver Operating Characteristic curve (ROC) to determine the optimal class boundary. This is the location in the curve that maximizes the area given the trade off between sensitivity and specificity (false positives and false negatives).
The pROC package provides a nice framework for generating ROC curves and AUC (Area Under the Curve) scores.
There is no need to accept this suggestion, for a model where the use case is mine detection and consequences are severe we might prefer to have fewer false negatives than false positives. This decision depends on relative cost of both types of error, but in this case we will use the optimal value of 0.227.
library(pROC)
Pen.pred <- predict(Pen.glm, newdata = test, type = "prob")
colnames(Pen.pred) <- c("No", "Yes")
Pen.cmx <- data.frame(Actual = test$Exited,
Prediction = Pen.pred$Yes) ## Fitted vals for ROC curve
Pen.proc <- roc(Pen.cmx$Actual, Pen.cmx$Prediction,
smoothed = T,
ci = T,
ci.alpha = 0.9, stratified=F,
plot=T, auc.polygon=T, max.auc.polygon=T, grid=T,
print.auc=T, show.thres=T,
print.thres=T)
Pen.cmx <- data.frame(Actual = test$Exited,
Prediction = ifelse(Pen.pred$Yes >= 0.227,1,0))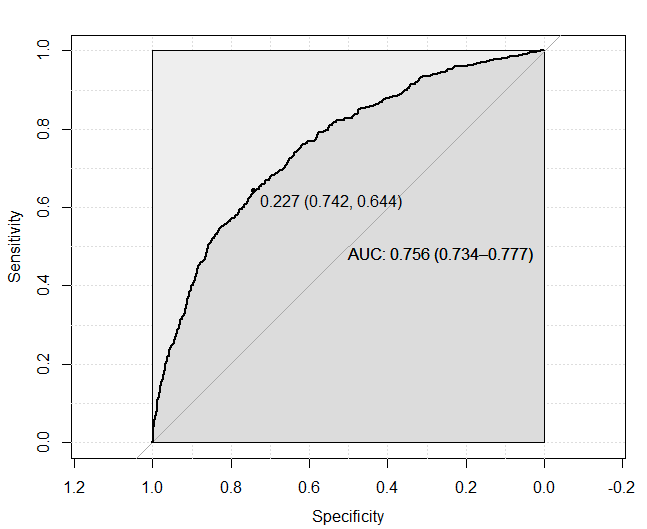
The AUC of our model is 0.756 or 76% of the area. A score above 80 would be a lot better, 76% indicates that our model either needs some work or is missing important explanatory variables.
Perhaps a future article will explore this dataset with a decision tree model, but we will leave it as is for the time being and pretend that this score meets the needs of our application.
Confusion Matrix
Next we will create a confusion matrix with the confusionMatrix function from the caret package. The ironically named confusion matrix is a popular tool for classification models that highlights accuracy and different types of classification errors.
We will also bring out our test data that represents 30% of our original dataset and see how our model performs on this holdout data it has never seen before.
confusionMatrix(as.factor(Pen.cmx$Prediction),
as.factor(Pen.cmx$Actual), positive = "1")
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 1776 221
1 613 391
Accuracy : 0.7221
95% CI : (0.7057, 0.7381)
No Information Rate : 0.7961
P-Value [Acc > NIR] : 1
Kappa : 0.3087
Mcnemar's Test P-Value : <0.0000000000000002
Sensitivity : 0.6389
Specificity : 0.7434
Pos Pred Value : 0.3894
Neg Pred Value : 0.8893
Prevalence : 0.2039
Detection Rate : 0.1303
Detection Prevalence : 0.3346
Balanced Accuracy : 0.6911
'Positive' Class : 1 The caret confusion matrix comes with a lot of other useful information and a confidence internal for accuracy which has a reasonable 3% spread in this case.
For imbalanced classes such as this dataset we can look to the Kappa value which gives an idea of how our model accuracy performs above random chance. In this case that is not great at 0.31 and that is because if we guessed randomly we’d be right more often than we are wrong simply because of the class distribution.
Although Kappa is interesting to note it’s not that useful as we are looking at our test data, and have already determined the optimal class boundary for our model based on AUC. The question at this point is really one of cost-tradeoffs on anticipated real world performance.
For customer churn we are not that concerned with accuracy or false positives unless marketing intervention is expensive. What we are more concerned about is failing to predict churn and having a customer leave since that has a much larger cost.
We want to focus more on the specificity score which represents the ability of the model to distinguish members that do not belong to the class, in other words where the model predicts the customer will remain, but the customer actually churns.
In our case the false positive rate is (1 – Specificity) or about 26% which is an improvement over no model but leaves a lot to be desired since we will miss 1 in 4 potential customers at risk.
Final Churn Model
Notwithstanding the mediocre performance we will proceed to tune our final model, this time using the entire dataset to get the best model possible, again using 10-fold cross validation.
We will however not create a new ROC curve, instead we will use the optimal cutoff we found on the test set after cross validation so our model can generalize better to new data.
We will also check out the confusion matrix for the final model.
Pen.glm.final <- train(
factor(Exited) ~ CreditScore + Geography + Gender + Age + Tenure + Balance + NumOfProducts + IsActiveMember,
data = ChurnData,
method = "glmnet",
family = "binomial",
preProc = c("zv", "center", "scale"),
trControl = trainControl(method = "cv", number = 10),
tuneLength = 20
)
mean(Pen.glm.final$resample$Accuracy)
Pen.glm.final$bestTune
Pen.pred <- predict(Pen.glm.final, newdata = ChurnData, type = "prob")
colnames(Pen.pred) <- c("No", "Yes")
Pen.cmx <- data.frame(Actual = ChurnData$Exited,
Prediction = ifelse(Pen.pred$Yes >= 0.227,1,0))
confusionMatrix(as.factor(Pen.cmx$Prediction), as.factor(Pen.cmx$Actual), positive = "1")Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5982 713
1 1981 1324
Accuracy : 0.7306
95% CI : (0.7218, 0.7393)
No Information Rate : 0.7963
P-Value [Acc > NIR] : 1
Kappa : 0.3257
Mcnemar's Test P-Value : <0.0000000000000002
Sensitivity : 0.6500
Specificity : 0.7512
Pos Pred Value : 0.4006
Neg Pred Value : 0.8935
Prevalence : 0.2037
Detection Rate : 0.1324
Detection Prevalence : 0.3305
Balanced Accuracy : 0.7006
'Positive' Class : 1
Our final model has a better accuracy measure than we saw during training, but real world performance will more likely resemble the score on our validation set since that data has never been seen before.
Saving Models
It is always a good idea to save our models in case we need to come back to them. It can be helpful for classification models to note the class cutoff in the file name since the chart will vanish once the R session has closed.
saveRDS(Pen.glm.final, "My-Churn-Model-227")Conclusion
Identifying customers who appear to be at risk of churning can help increase customer lifetime value and maximize the benefit of our acquisition costs. Logistic regression can be a simple and effective way of predicting customer churn in many cases.
Although the model struggled with this particular dataset we might improve that with class weightings before trying a more advanced but less interpretable option.
Happy modeling!
References
Chapmen, C.; McDonnell Feit, E. R for Marketing Research and Analytics; Springer, 2015.
Dunn, P.; Smyth, P. Generalized Linear Models With Examples in R; Springer, 2018.
Gelman A.; Hill J. Data Analysis Using Regression and Multilevel/Hierarchial Models; Cambridge, 2007.
Recent Post
Excel Histograms
- 31 August 2025
- 3 min read
Combine Data in Excel with Power Query
- 31 July 2025
- 6 min read
Excel Radar Charts for Demographics
- 28 June 2025
- 3 min read
Writing Unstructured Data with Sink in R
- 25 May 2025
- 4 min read
Sales Lift Estimation with tools4uplift
- 30 April 2025
- 11 min read








