Business Insights
The thing we are interested in often depends on other things, sometimes a lot of other things.
Feature selection tools can help us determine which variables are important, but where we are interested in assessing causal relationships between variables it is more insightful to use network graphs called DAGs.
We can rely on structure learning algorithms in conjunction with our experts to put together a model of reality. Not only can this result in a useful decision tool, the process itself can be very insightful.
Let’s explore using an Additive Bayesian Model to determine what factors influence car prices on behalf of a fictitious client interested in entering the North American market.
Results
We determine that price depends on car width, cylinder number, and engine size; and does not directly depend on city mileage. Further, we can project that the median price of a six cylinder vehicle will be around $29,000.
Follow along below in R Studio to see how we arrived at this result.
Dataset
We will use a Kaggle dataset that lists car prices based on an assortment of features such as length, horsepower, and city mileage.
Data Loading
We’ll first load our car price dataset with strings as factors and run a summary. We won’t reproduce the summary but it does not show any missing values.
Next we will wipe out curbweight by setting the column to NULL. As it turns out, curb weight has a lot of correlation with car price, but logically we would not expect customers to pay more for a car just because it is heavier.
CarPrices <- read.csv("CarSales.csv", stringsAsFactors = T)
summary(CarPrices)
CarPrices$curbweight <- NULL
CarPrices$cylindernumber <- factor(CarPrices$cylindernumber)Feature Selection
Even after curbweight’s untimely demise, we still have 25 variables to contend with. We can also ignore the ID, symboling (insurance risk rating), and car make. Although brand may impact price it’s not relevant to a foreign client looking to develop a new car for the market. For risk rating, we can assume that high risk is not going to be a conscious design decision.
After removing a couple questionable variables a good approach for a large dataset is to use a feature selection algorithm. We will try Relief from the F-Selector package. This is a popular choice using a k-nearest neighbours approach to measure feature importance.
Relief zones in on a few response values and looks for the predictors that do the best job distinguishing between them. Those features are rewarded with points, and features that fare less well are penalized.
Relieved <- relief(price ~ ., CarPrices[,c(4:25)])
Relieved$Names <- rownames(Relieved)
sort(Relieved, decreasing = T) attr_importance Names
enginetype 0.1489182313 enginetype
drivewheel 0.1051807986 drivewheel
cylindernumber 0.0458980652 cylindernumber
carlength 0.0369936755 carlength
horsepower 0.0350718058 horsepower
wheelbase 0.0320561990 wheelbase
aspiration 0.0317388015 aspiration
peakrpm 0.0277343810 peakrpmRelief seems to be a fan of large engines but also zeros in on citympg and carlength.
Next we will try an alternative from the Varrank package (variable rank) and see what it comes up with. This is a great package that allows a lot of control over ranking algorithms. We will use the “peng” method because it’s faster than the default.
Varrank uses a Minimum Redundancy Maximum Relevancy (mRMRe) approach to variable selection. It ranks features based on how much additional information they contribute over the first feature and down the entire list.
Rankings <- varrank::varrank(
data.df = CarPrices[, c(4:25)],
method = "peng",
variable.important = "price",
discretization.method = "sturges",
algorithm = "forward",
scheme = "mid",
verbose = FALSE
)
plot(Rankings)
summary(Rankings)
diag(Rankings$distance.m)We can get a descending summary of rankings. A trick to minimize the verbosity is also just take take the diagonal of the ranking matrix. Plotting the output is even more helpful.
Following down the diagnal we can see the importance scores in descending order from carwidth (0.737), citympg(0.229), and down to stroke.
This is an interesting approach popularized by some data scientists at Uber. In this case the results are not that different between methods, and it’s not surprising that features which can distinguish between similar response variables will probably contain more information.
For a network graph model where parsimony is very important and redundancy will likely have negative consequences, this a good approach to consider for variable selection.
Notably, Stroke is considered redundant by mRMRe, suggesting that knowing stroke volume contains no information if we already know engine size, horsepower, and cylindernumber.
Variable Selection
We will select some of the top tier variables to try build out a structural model for car prices. Specifically, carwidth, citympg, carbody (e.g. sedan), enginesize, and price as our response variable.
Since price follows a non-parametric (bell shaped) distribution and tends to be non-negative we will want to model this with a Poisson distribution. To avoid causing fitting issues we will scale this down by $1,000 and convert it to an integer.
CarMod <- select(CarPrices, carwidth, citympg, carbody, enginesize, cylindernumber, price)
CarMod <- mutate(CarMod, price = as.integer(round(price)/1000))ABN Package
The abn package specializes in structural learning using additive bayesian networks, and unlike other R packages is more flexible in terms of being able to select the probability distributions for different nodes.
Our first task with abn now that we have narrowed down our search space to some of the more relevant variables is to specify the distributions. Each node of the model will be a regression equation, so for example, citympg will be predicted by its parent nodes and some coefficients.
Citympg is a good candidate for a Poisson response because it is low value counts with positive values. We will go with this for price as well. Otherwise we will choose Gaussian (normal) response variables, and multinomial for carbody and cylindernumber.
Note that choosing a multinomial variable excludes us from using “bayes” as a structure learning method so we will have to specify maximum likelihood instead (“mle”).
dists <- list(
carwidth = "gaussian",
citympg = "poisson",
carbody = "multinomial",
enginesize = "gaussian",
cylindernumber = "multinomial",
price = "poisson"
)Next we have to create a score cache which helps defines the model structure based on the parameters we specify. We will limit to a maximum of 3 parents to save computation time, and also to avoid a messy model that is impossible to interpret.
The score cache is used by the mostProbable function to learn the network structure. There is an alternative hill climbing algorithm available if needed, particularly if it takes too long. That is a likely outcome of using too many nodes because the number of possible combinations explodes rapidly.
cache <- buildScoreCache(CarMod[,1:6], data.dists = dists, method = "mle", max.parents = 3)
network <- mostProbable(cache)
network
plotAbn(network)Our new network contains an adjacency matrix indicating for rows the outgoing edges and columns the incoming edges. We can also plot our network with plotAbn.
carwidth citympg carbody enginesize cylindernumber price
carwidth 0 0 0 0 0 0
citympg 1 0 0 0 0 0
carbody 0 0 0 0 0 0
enginesize 1 0 0 0 1 1
cylindernumber 0 1 0 0 0 1
price 1 1 1 0 0 0
Consensus DAG from 'mostprobable', can be use with 'fitAbn'.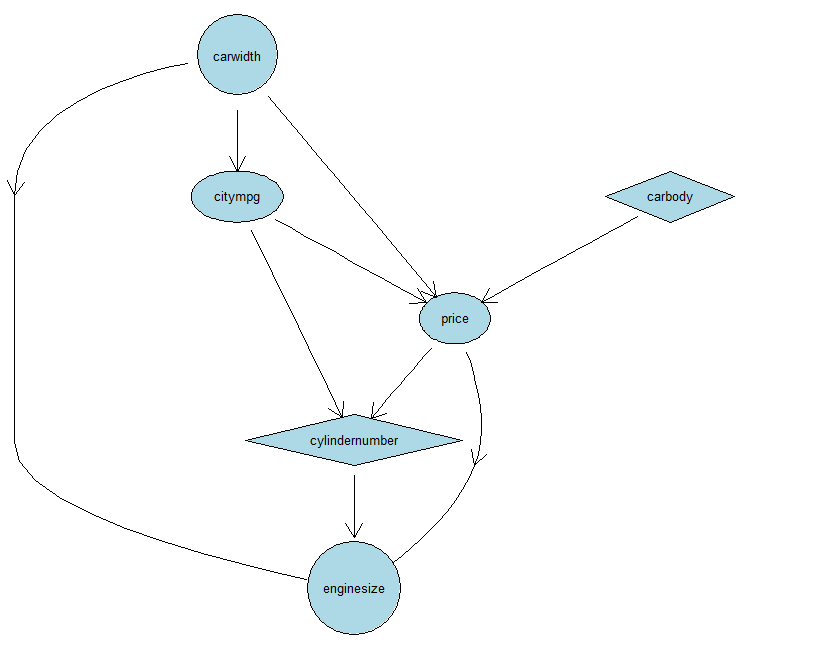
Not a bad first effort. Although it would be fair to say engine size depends on price, we are actually interested in the effect of variables on price not the other way around.
We will need to tell the model that nothing depends on price, and also include some expert knowledge to help our model along.
Ban/Retained Matrices
The package handles these details by allowing the user to specify a ban matrix and a retain matrix. It is also possible to use a formula such as (~price | .) for price depends on everything, but for multiple conditions we build a matrix.
The first step is to ban all edges from leaving price. We can accomplish this by creating a matrix with row and column names matching our distributions. Then we can set all columns in price to 1, indicating that “nothing can depend on price.”
### Network Bans
ban.mat <- matrix(0, nrow = 6, ncol = 6, dimnames = list(names(dists), names(dists)))
ban.mat[,"price"] <- 1
ban.matNext we will build our matrix of retained edges based on some admittedly less than exceptional knowledge of vehicles.
This time we will specify that “citympg depends on enginesize” by placing a one in the same row as citympg and the same column as enginesize. Next we’ll ensure that carwidth and tweak a few other parameters for good measure. Seems reasonable.
### Retained Edges
### X depends on Y
retain.mat <- matrix(0, nrow = 6, ncol = 6, dimnames = list(names(dists), names(dists)))
retain.mat["citympg", c("enginesize")] <- 1
retain.mat["carwidth", c("carbody")] <- 1
retain.mat["carbody", c("enginesize")] <- 1
retain.mat["cylindernumber", c("enginesize")] <- 1
We will have to rebuild our score cache after making these changes. this time specifying dag.banned and dag.retained as the two matrices we created.
cache <- buildScoreCache(
CarMod[, 1:6],
data.dists = dists,
method = "mle",
max.parents = 3,
dag.banned = ban.mat,
dag.retained = retain.mat
)
network <- mostProbable(cache)
network
plotAbn(network)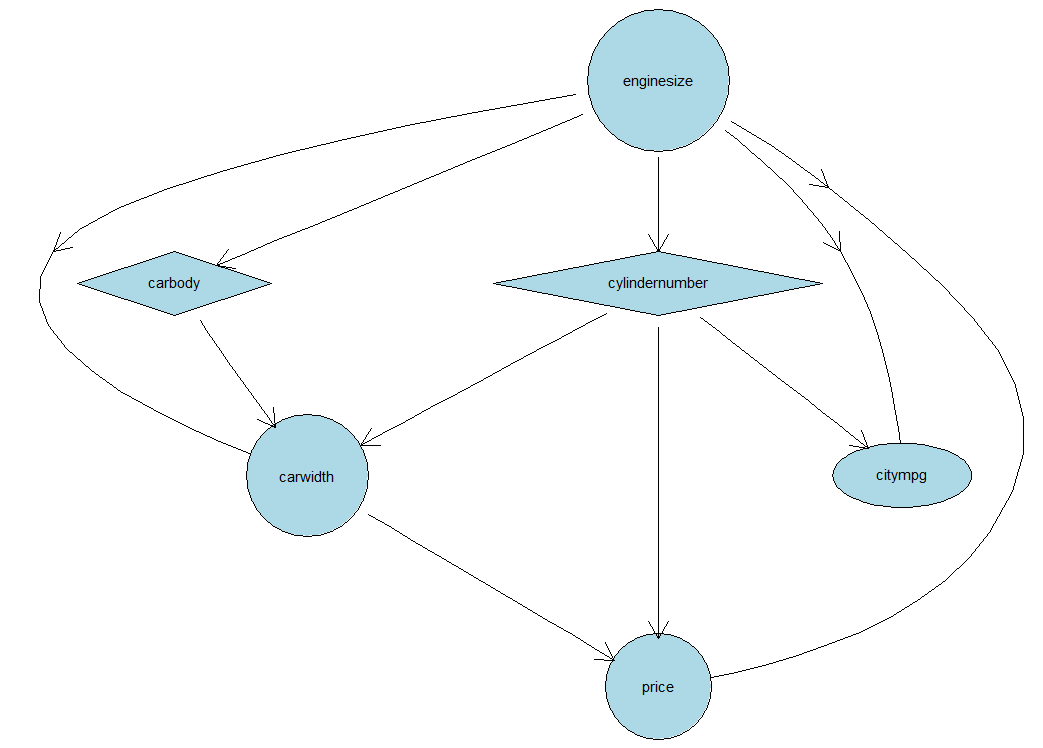
Our model is looking ok after a few tweaks, it suggests that price will depend on engine size, width, and the number of cylinders.
Model Fitting
Once we have settled on a structure we can fit our model in order to determine the coefficients for each node. The model is written in BUGS language which can be viewed by setting verbose=True in the fitAbn() function.
Note that continuous numeric variables are centered and scaled before fitting the model, so in order to make predictions new values have to be scaled, and to validate the responses we will have to put things back on the original scale.
To do that we find the mean of the original variables and their standard deviations and then unscale them. Variable * SD + Mean.
The fitting functionality in this package is designed for structural learning rather than inference, but we can have a bit of fun with it and also test whether the model is generating realistic data which will be important before adopting it.
fit <- fitAbn(network, method = "mle")
summary(fit)Simulating the Network
To run a network simulation using Gibbs sampling we just need to run the simulateAbn function, and we can set the number of iterations to 1,000,000 to give us something to work with.
CarSim<- simulateAbn(fit, verbose = T, n.iter = 1000000L)
head(CarSim) carbody carwidth citympg cylindernumber enginesize price
1 4 6.015839 27 3 -0.7960471 23
2 3 6.491250 216 5 -1.5570122 0
3 2 7.398326 54 4 0.8716608 21
4 3 5.593396 32 3 -0.2563949 14
5 4 9.725772 1595 7 -1.4447183 0
6 3 5.278189 29 3 -0.5087861 18Since some variables have been scaled, we will need to reverse this treachery before getting any answers. We can use the apply function to find the means and standard deviations.
CarMeans <- apply(CarMod[,c(1,4)], MARGIN = 2, FUN = mean)
CarSD <- apply(CarMod[,c(1,4)], MARGIN = 2, FUN = sd)
CarMeans
CarSD> CarMeans
carwidth enginesize
65.9078 126.9073
> CarSD
carwidth enginesize
2.145204 41.642693 We will next create a function to unscale our variables and replace the simulation output with the unscaled versions for analysis. For price we will simply multiply it back by $1,000.
CarSim$enginesize <- unscale(CarSim$enginesize, CarMeans[2], CarSD[2])
CarSim$carwidth <- unscale(CarSim$carwidth, CarMeans[1], CarSD[1])
CarSim$price <- CarSim$price * 1000
quantile(CarSim$price)
quantile(CarSim$carwidth)
quantile(CarSim$citympg)> quantile(CarSim$price)
0% 25% 50% 75% 100%
0 19000 29000 40000 158000
> quantile(CarSim$carwidth)
0% 25% 50% 75% 100%
70.50387 78.77064 80.69733 83.23874 93.01636
> quantile(CarSim$citympg)
0% 25% 50% 75% 100%
0 18 23 37 1692 Car price seems to have a reasonable range but is centered a bit high and the minimum is zero. That could be a vehicle no-one wants to buy, or a modeling issue.
Car width seems a bit large but considering that our simple model is trying to predict it from cylinder number and car body it’s not that far off.
We can plot the price points to check how well our model is generating data compared to the process it is supposed to be modeling.
hist(CarSim$price, breaks = 40, main = "Vehicle Prices (small model)", xlab = "Price ($)")
hist(CarPrices$price, breaks = 40, main = "Vehicle Prices (original)", xlab = "Price ($)")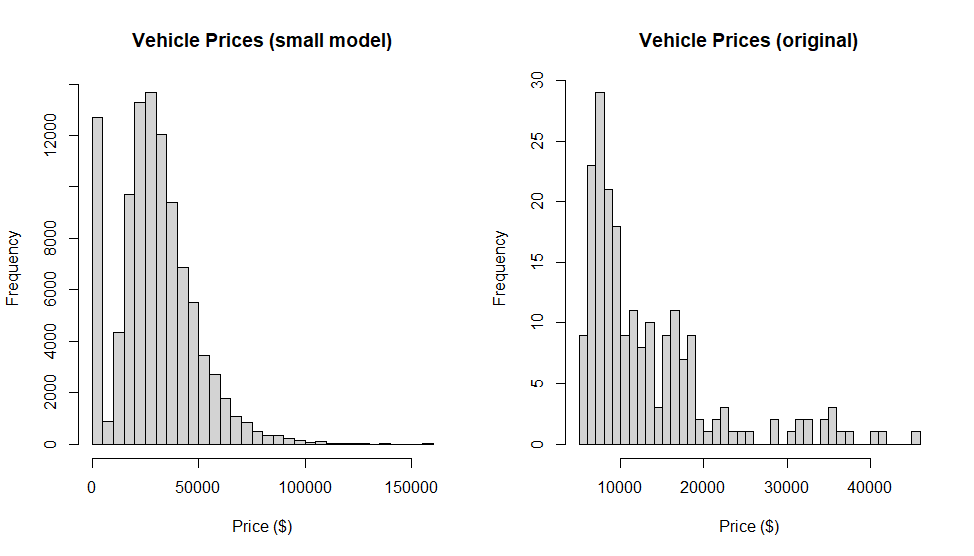
Unfortunately, the overall price estimates seem much higher than they should be which suggests we may have to make adjustments. There are also a lot of zero values being generated which seems incorrect.
A Larger Model
Without getting too carried away with reparametrization we can change some of the above code and include additional variables to see if this improves performance.
This time we will set cylinder number to Poisson to represent it as small count values. We include more of the relevant variables. and remove variables with more than two categories so we can use a Bayesian algorithm rather than maximum likelihood.
CarMod <- select(CarPrices, carwidth, citympg, enginesize, cylindernumber, horsepower, carlength, highwaympg,
aspiration, wheelbase, price) %>% mutate(cylindernumber = case_when(
cylindernumber == "one" ~ 1,
cylindernumber == "two" ~ 2,
cylindernumber == "three" ~ 3,
cylindernumber == "four" ~ 4,
cylindernumber == "five" ~ 5,
cylindernumber == "six" ~ 6,
cylindernumber == "seven" ~ 7,
cylindernumber == "eight" ~ 8,
cylindernumber == "twelve" ~ 12
))
CarMod <- mutate(CarMod, price = as.integer(round(price)/1000))
dists <- list(
carwidth = "gaussian",
citympg = "poisson",
enginesize = "gaussian",
cylindernumber = "poisson",
horsepower = "poisson",
carlength = "gaussian",
highwaympg = "poisson",
aspiration = "binomial",
wheelbase = "gaussian",
price = "poisson"
)
### Network Bans
ban.mat <- matrix(0, nrow = 10, ncol = 10, dimnames = list(names(dists), names(dists)))
ban.mat[,"price"] <- 1
ban.mat["carlength", c("highwaympg", "citympg")] <- 1
ban.mat["horsepower", c("citympg", "highwaympg")] <- 1
### Retained Edges
### X depends on Y
retain.mat <- matrix(0, nrow = 10, ncol = 10, dimnames = list(names(dists), names(dists)))
retain.mat["citympg", c("enginesize")] <- 1
retain.mat["cylindernumber", c("enginesize")] <- 1Next we will cache our model with “bayes” as the method and repeat similar steps to fit, simulate, and rescale our target variable. We also provide more flexibility by allowing a maximum of five parent nodes.
cache <- buildScoreCache(
CarMod,
data.dists = dists,
method = "bayes",
max.parents = 5,
dag.banned = ban.mat,
dag.retained = retain.mat
)
network <- mostProbable(cache)
network
plotAbn(network)
## Fit the DAG
fit <- fitAbn(network, method = "bayes")
summary(fit)
fit
CarSim<- simulateAbn(fit, verbose = T, n.iter = 1000000L)
head(CarSim)
CarSim$price <- CarSim$price * 1000
quantile(CarSim$price)
par(mfrow = c(1,2))
hist(CarSim$price,
breaks = 40,
main = "Vehicle Prices (full model)",
xlab = "Price ($)")
hist(CarPrices$price,
breaks = 40,
main = "Vehicle Prices (original)",
xlab = "Price ($)")
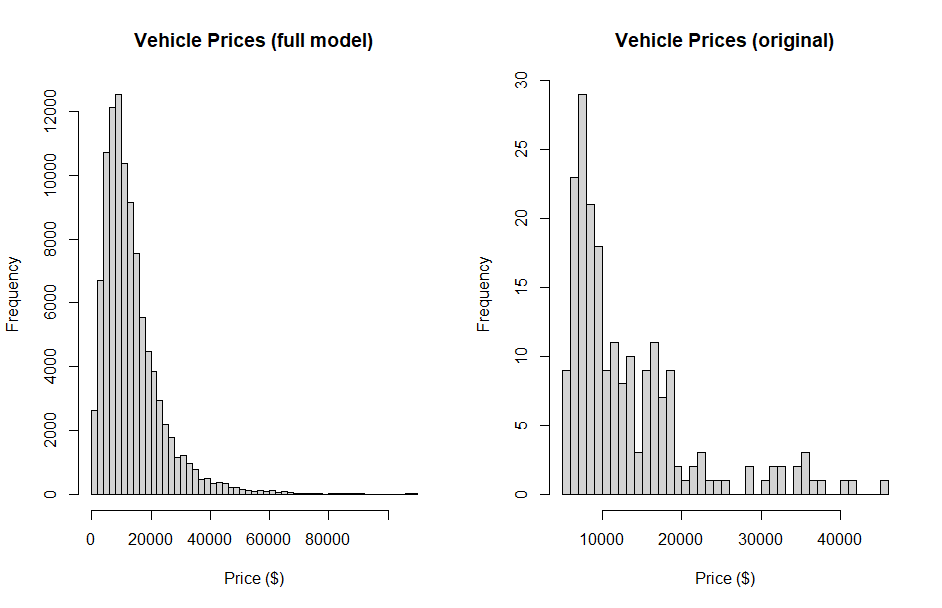
Providing abn with additional relevant variables, modeling flexibility, and using the Bayesian approach looks to have produced better target estimates. Price now depends on citympg, carwidth, and enginesize.
Most of the relationships seem reasonable, for example, car width depends on length and engine size. We did specify a few key constraints to help the model along but they were few in number. However, we were careful not to be presumptive about what price depends on because that was our target.
Conclusion
Structure learning can be a fun exercise to help understand relationships between different variables. It can also be a frustratingly iterative process but it also forces us to think about dependency relationships and consider new possibilities. This process allows for the inclusion of human expertise, and can be a very insightful approach.
The abn package is very flexible but the documentation is a bit light as it is in early development. It is currently the only R package that allows for specifying a wide range of node distributions.
References
Scrutari, Marco; Jean-Baptiste, Denis. Bayesian Networks, 2nd Edition. Chapman & Hall/CRC, 2021.
Related Posts
Bayesian Networks in Services Marketing explores a simple pre-defined Bayesian model in the context of services marketing.
